FUNCIÓN INVERSA EN DIAGRAMA SAGITAL

Definición.

 

Se llama función inversa,  , de una función f a una nueva función cuyo dominio es la imagen de la función inicial, y su imagen es el dominio de la función inicial. Es decir, si la función g es la función inversa de f, entonces se cumple que si f (b) = a, entonces g(a)=b.

 La función inversa no siempre existe. Las únicas funciones que tienen inversa son las 

FUNCIONES BIYECTIVAS.

  

EJEMPLO 1

La función f  NO TIENE INVERSA ya que  NO ES INYECTIVA , por lo tanto no es BIYECTIVA, y únicamente las FUNCIONES BIYECTIVAS tienen INVERSA.

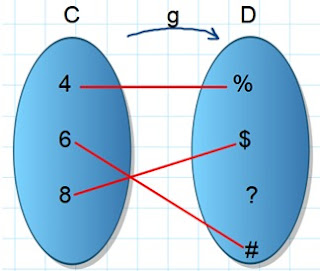
 EJEMPLO 2

La función g  NO TIENE INVERSA ya que  NO ES SOBREYECTIVA , por lo tanto no es BIYECTIVA , y únicamente las FUNCIONES BIYECTIVAS tienen INVERSA.

EJEMPLO 3                                                                 

La función f   TIENE INVERSA ya que  f es INYECTIVA y también f es SOBREYECTIVA , por lo tanto es BIYECTIVA , y únicamente las FUNCIONES BIYECTIVAS tienen INVERSA.

EJERCICIO ´PRÁCTICO

Hallar la función inversa de f, y ubicarlos en un diagrama sagital   

 EJERCICIO PRÁCTICO

Tabular en un conjunto la función inversa de f del ejercicio anterior , que se muestra en el siguiente diagrama de Venn.

 EJERCICIO PRÁCTICO

Hallar la función inversa de h (x).